密码学入门

古典密码

凯撒

替换加密算法，26个字母在表上循环，向前或向后移n个字母。加密后移，解密前移。凯撒

变异凯撒

替换加密算法，循环顺序变为在ascii码表上循环。

维吉尼亚加密

有字母表作为对照

假设明文是ATTACK，密钥是CAT，加密将密钥重复至与明文相同长度，CATCAT，一一对应查表加密。密文则是CTMCCD。

词频分析

一段文章里，特定的字母出现的频率基本固定不变。比如字母e出现的频率最高，为0.12702，就可以分析密文的字母频率还原明文。

或者知道替换字母，比如MTHJ{CUBCGXGUGXWREXIPOYAOEYFIGXWRXCHTKHFCOHCFDUCGTXZOHIXOEOWMEHZO}，quipqiup

现代密码

现代密码与古典密码的区别就是加密算法是否公开的区别。

理论安全与实际安全

理论安全，或无条件安全：攻击者无论截获多少密文，都无法得到足够的信息来唯一地决定明文。Shannon用理论证明：欲达理论安全，加密密钥长度必须大于等于明文长度，密钥只用一次，用完即丢，即一次一密。

实际安全，或计算上安全：如果攻击者拥有无限资源，任何密码系统都是可以被破译的；但是，在有限的资源范围内，攻击者都不能通过系统的分析方法来破解系统，则称这个系统是计算上安全的或破译这个系统是计算上不可行。

分组密码：DES

明文加密16轮，初始的密钥经过16轮变换产生16个子密钥用来加密每一轮产生的密文。

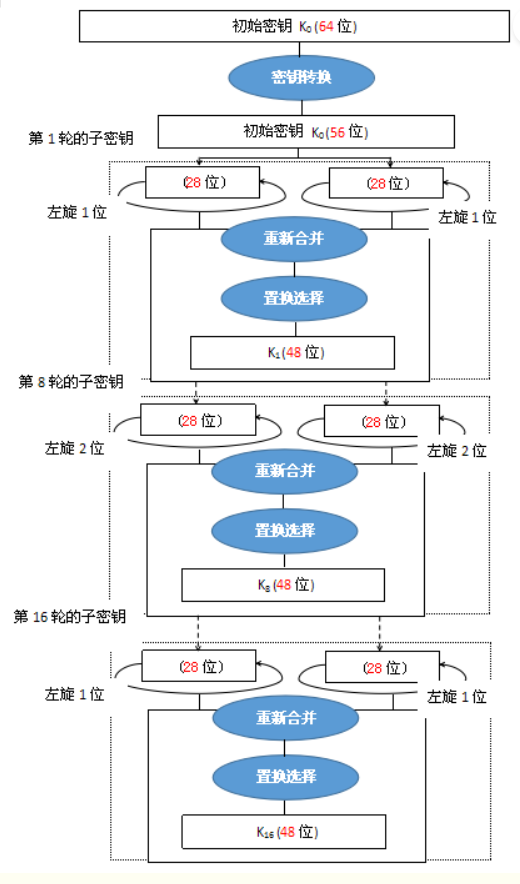
密钥转换与左旋位数有转换表作为对照。

加解密过程

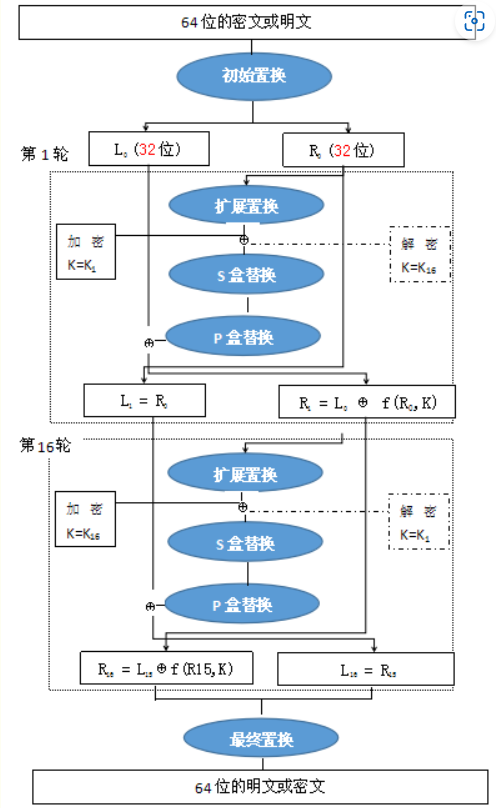
DES已经被证明是不安全的，密钥可以通过穷举找出。现在一般采用3DES或者AES。

分组密码的工作模式

电子密码本模式，ECB

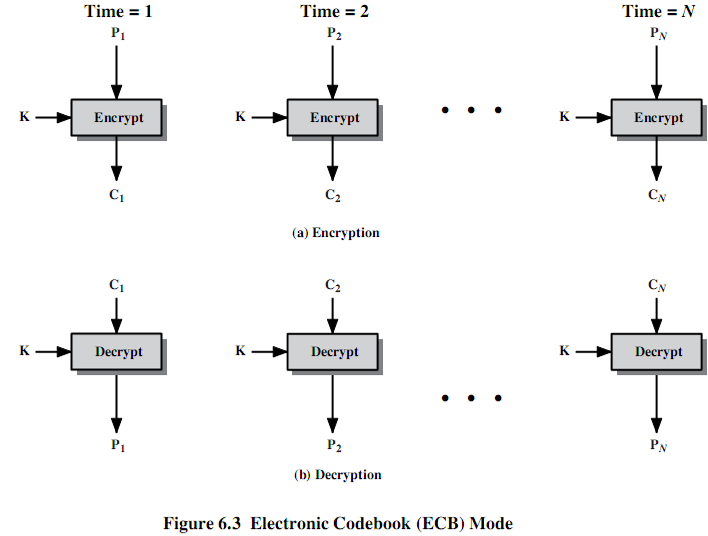
ECB模式特别适合数据较少的情况，如安全传输密钥。一段明文消息中若有几个相同的明文组，则密文也将出现几个相同的片段。对于很长的消息，ECB是不安全的，如果消息是非常结构化的，密码分析可能利用其结构特征来破解。

密文分组链接模式 CBC

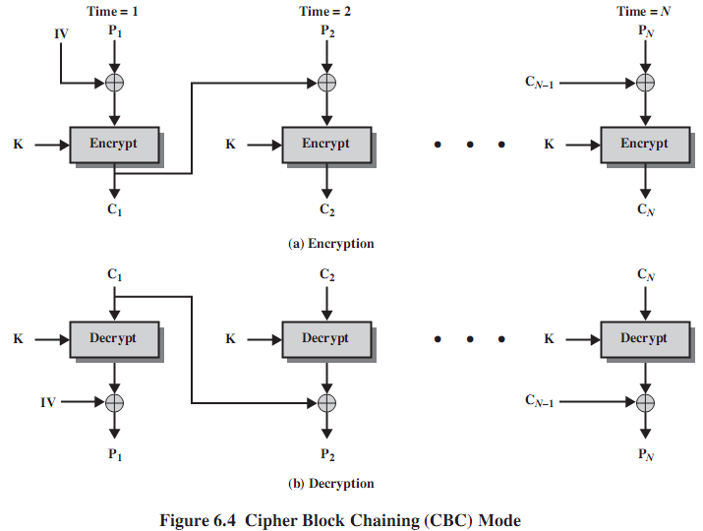
加密输入是当前明文分组和前一密文分组的异或

密码反馈模式 CFB

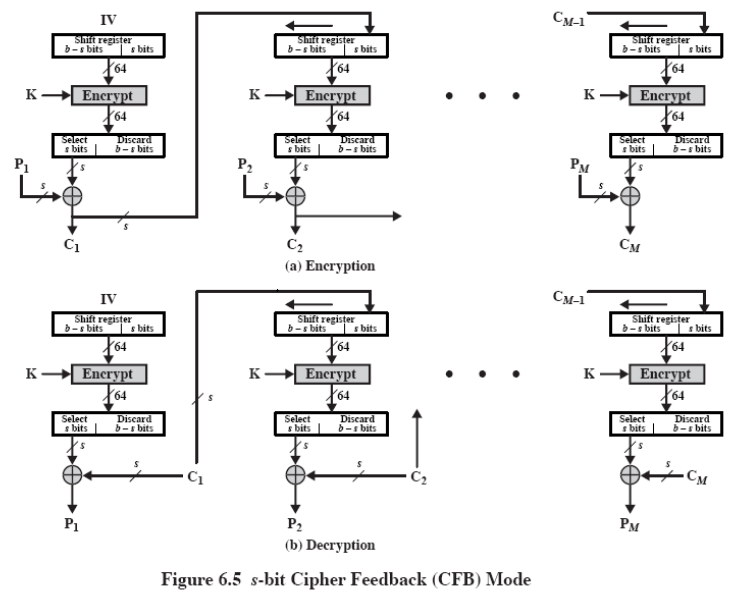
先加密初始向量再异或，异或结果作为下一轮密钥

输出反馈模式 OFB

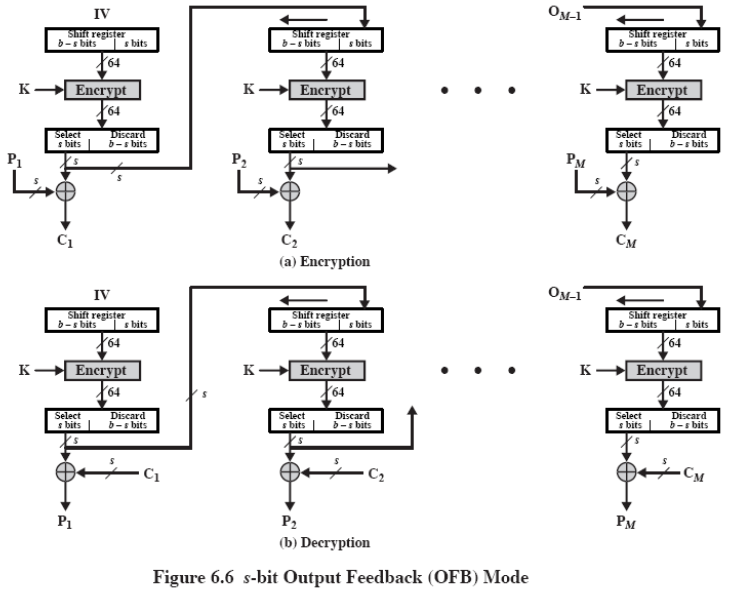
加密结果作为下一轮密钥

公钥密码：RSA

RSA是ctf比赛中最常见的加密算法，有多种多样的攻击方式。

加解密算法

\[ 费马小定理：若p是素数，a是正整数且不能被p整除，则a^{p-1}modp \equiv 1，那么a^{p}modp \equiv a\\ 欧拉函数：\phi(n)的值是从1到n-1和n互质的数的数量。\\ 显然，对于质数n \phi(n)=n-1，如果n为两个质数p和q的乘积，\phi(n)=(p-1)*(q-1).\\ 欧拉定理：对于任意互质的a和n有：a^{\phi(n)}\equiv1modn.\\ RSA加密算法：随机选择两个大素数p和q，计算n=p*q以及phi=(p-1)*(q-1).\\ 选择一个与\phi(n)互质的数e作为加密指数，对e求关于phi的逆作为d，即ed\equiv1mod\phi(n).\\ 加密：c=m^emodn\\ 解密：m=c^dmodn=(m^emodn)^dmodn=m. \]

公钥密码：Elgamal

假设A和B互相通信，共享大素数p，本原元素\(\alpha\)，明文m<p，通信时A的私钥为\(x_a\)，公钥为\(Y_a=\alpha^{x_a}modp\)，B的私钥为\(x_b\)，公钥为\(Y_b=\alpha^{x_b}modp\)，A向B发送消息，计算K=\(Y_b^{x_a}modp\)=\(\alpha^{x_ax_b}modp\)，\(c_1=\alpha^{x_a}modp，c_2=mKmodp\)，密文即为(\(c_1，c_2\))。

B收到信息后，首先恢复K，K=\(c_1^{x_b}modp\)，然后m=\(c_2/Kmodp\).

每次随机选择私钥发送信息，同样的密文每次加密出不同的密文。

公钥密码：ECC

最简单的一类椭圆曲线：\(y^2=x^3+ax+b\).

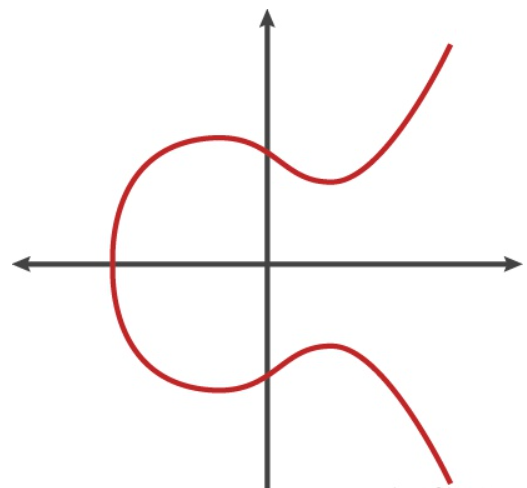
加法与乘法的定义：连线与切线。

加密时，A选取一条椭圆曲线\(E_p(a,b)\)并选择其中一点G，选取私钥k计算kG作为公钥。

A将E，K，G发送给B。

B将明文m转换为E上的一个点M，并生成一个随机数r，计算\(c_1=M+rK，c_2=rG\)，发送\(c_1,c_2\)

A计算\(c_1-kc_2\)即可解密。

格密码

涉及线代知识，目前阶段不作为重点。

作业

   # flag * 2 ** 10000 mod 10**175 = x
   # flag * 2 ** 10000 = y * 2 ** 175 + k * 10 ** 175
   # flag * 2 ** 9825 = y mod 5 ** 175
   print(gmpy2.invert(2 ** 9825, 5 ** 175))
   y = 1473327817893791860679080635376845598464916175771199125558742418628097409377550464912703622357336416382120404612476355317875179245511879304348013049276070451780858374753615872 // (2 ** 175)
   print(y)
   flag = y * gmpy2.invert(2 ** 9825, 5 ** 175) % (5 ** 175)
   print(long_to_bytes(flag))

sha & CTF记录

第三次例会-密码学入门